Stoichiometry Worksheet 1 Mass Mass

This is a comprehensive, end-of-chapter fix of practice problems on stoichiometry that covers balancing chemic equations, mole-ratio calculations, limiting reactants, and pct yield concepts.

The links to the corresponding topics are given below.

• The Mole and Molar Mass
• Molar Calculations
• Per centum Limerick and Empirical Formula
• Stoichiometry of Chemical Reactions
• Limiting Reactant
• Reaction/Percent Yield
• Stoichiometry Exercise Issues

Practice

1.

Balance the following chemical equations:

a) HCl + O₂ → H_twoO + Cl₂

b) Al(NO₃)₃ + NaOH → Al(OH)₃ + NaNO_iii

c) H₂ + N₂ → NH₃

d) PCl₅ + H_iiO → H₃PO_four + HCl

east) Fe + H₂SO_four → Fe₂(SO₄)₃ + H_ii

f) CaCl₂ + HNO₃ → Ca(NO₃)₂ + HCl

yard) KO₂ + H_iiO → KOH + O₂ + H₂O₂

h) Al + H₂O → Al₂O₃ + H₂

i) Fe + Br_two → FeBr₃

j) Cu + HNO_three → Cu(NO₃)₂ + NO₂ + H₂O

m) Al(OH)₃ → Al₂O₃ + H₂O

l) NH₃ + O₂ → NO + H_twoO

one thousand) Ca(AlO₂)₂ + HCl → AlCl₃ + CaCl₂ + H₂O

n) C₅H₁₂ + O_ii → CO₂ + H_twoO

o) P_ivO₁₀ + H₂O → H₃PO₄

p) Na_twoCrO₄ + Pb(NO₃)_two → PbCrO₄ + NaNO₃

q) MgCl₂ + AgNO₃ → AgCl + Mg(NO₃)₂

r) KClO₃ → KClO₄ + KCl

due south) Ca(OH)₂ + H₃PO₄ → Ca_three(PO_iv)₂ + H₂O

a)

answer

2HCl + O₂ → H_iiO + Cl₂

b)

reply

Al(NO_iii)_iii + 3NaOH → Al(OH)₃ + 3NaNO₃

c)

respond

3H_ii + North_ii → 2NH₃

d)

reply

PCl_v + 4H_iiO → H₃PO₄ + 5HCl

e)

respond

2Fe + 3H_iiSO₄ → Iron₂(And so₄)_iii + 3H_ii

f)

answer

CaCl_ii + 2HNO_iii → Ca(NO₃)₂ + 2HCl

thou)

answer

2KO₂ + 2H_iiO → 2KOH + O₂ + H₂O₂

h)

answer

2Al + 3H₂O → Al_iiO₃ + 3H₂

i)

respond

2Fe + 3Br_two → 2FeBr_iii

j)

answer

Cu + 4HNO_iii → Cu(NO₃)₂ + 2NO₂ + 2H_iiO

1000)

respond

2Al(OH)_three → Al₂O₃ + 3H₂O

fifty)

respond

4NH_iii + 5O₂ → 4NO + 6H₂O

k)

answer

Ca(AlO_ii)₂  +  8HCl → 2AlCl₃ + CaCl₂ + 4H₂O

n)

reply

C₅H₁₂ + 8 O₂ → 5CO₂ + 6H₂O

o)

reply

P₄O_x + 6H₂O → 4H₃PO_iv

p)

answer

Na_twoCrO₄ + Pb(NO₃)₂ → PbCrO₄ + 2NaNO₃

q)

answer

MgCl₂ + 2AgNO₃ → 2AgCl + Mg(NO₃)₂

r)

answer

4KClO₃ → 3KClO₄ + KCl

south)

answer

3Ca(OH)₂ + 2H_threePO₄ → Ca_iii(PO_four)₂ + 6H₂O

2.

Consider the counterbalanced equation:

C₅H₁₂ + 8 O₂ → 5CO₂ + 6H_twoO

Complete the table showing the appropriate number of moles of reactants and products.

mol CvH12	mol Otwo	mol COii	mol HtwoO
two
	2.5
		3
			5.4

answer

C_fiveH₁₂ + 8 O₂ → 5CO_ii + 6H₂O

mol C5H12	mol Oii	mol CO2	mol H2O
2	16	10	12
0.3125	two.5	1.5625	1.875
0.half dozen	4.8	3	3.6
0.9	7.2	4.5	5.4

Solution

The moles of other molecules are calculated based on the stoichiometric ratio. For the start row the moles are calculated as follows:

\[{\rm{n}}\left( {{{\rm{O}}_{\rm{2}}}} \right)\;{\rm{ = }}\;{\rm{two }}\cancel{{{\rm{mol}}\;{{\rm{C}}_{\rm{5}}}{{\rm{H}}_{{\rm{12}}}}}}\;{\rm{ \times }}\;\frac{{{\rm{8}}\;{\rm{mol}}\;{{\rm{O}}_{\rm{two}}}}}{{{\rm{i}}\;\cancel{{{\rm{mol}}\;{{\rm{C}}_{\rm{5}}}{{\rm{H}}_{{\rm{12}}}}}}}}\;{\rm{ = }}\;{\rm{sixteen}}\;{\rm{mol}}\]

\[{\rm{n}}\left( {{\rm{C}}{{\rm{O}}_{\rm{2}}}} \right)\;{\rm{ = }}\;{\rm{2 }}\cancel{{{\rm{mol}}\;{{\rm{C}}_{\rm{five}}}{{\rm{H}}_{{\rm{12}}}}}}\;{\rm{ \times }}\;\frac{{{\rm{v}}\;{\rm{mol}}\;C{{\rm{O}}_{\rm{ii}}}}}{{{\rm{1}}\;\cancel{{{\rm{mol}}\;{{\rm{C}}_{\rm{5}}}{{\rm{H}}_{{\rm{12}}}}}}}}\;{\rm{ = }}\;{\rm{10}}\;{\rm{mol}}\]

\[{\rm{northward}}\left( {{{\rm{H}}_{\rm{2}}}{\rm{O}}} \right)\;{\rm{ = }}\;{\rm{ii }}\cancel{{{\rm{mol}}\;{{\rm{C}}_{\rm{five}}}{{\rm{H}}_{{\rm{12}}}}}}\;{\rm{ \times }}\;\frac{{{\rm{6}}\;{\rm{mol}}\;{{\rm{H}}_{\rm{2}}}{\rm{O}}}}{{{\rm{one}}\;\abolish{{{\rm{mol}}\;{{\rm{C}}_{\rm{5}}}{{\rm{H}}_{{\rm{12}}}}}}}}\;{\rm{ = }}\;{\rm{12}}\;{\rm{mol}}\]

For the 2d row :

\[{\rm{north}}\left( {{{\rm{C}}_{\rm{5}}}{{\rm{H}}_{{\rm{12}}}}} \right)\;{\rm{ = }}\;{\rm{2}}{\rm{.five }}\abolish{{{\rm{mol}}\;{{\rm{O}}_{\rm{two}}}}}\;{\rm{ \times }}\;\frac{{{\rm{ane}}\;{\rm{mol}}\;{{\rm{C}}_{\rm{5}}}{{\rm{H}}_{{\rm{12}}}}}}{{viii\;\abolish{{{\rm{mol}}\;{{\rm{O}}_{\rm{2}}}}}}}\;{\rm{ = }}\;{\rm{0}}{\rm{.3125}}\;{\rm{mol}}\]

\[{\rm{due north}}\left( {{\rm{C}}{{\rm{O}}_{\rm{2}}}} \right)\;{\rm{ = }}\;{\rm{2}}{\rm{.5 }}\cancel{{{\rm{mol}}\;{{\rm{O}}_{\rm{2}}}}}\;{\rm{ \times }}\;\frac{{{\rm{5}}\;{\rm{mol}}\;{{\rm{C}}_{\rm{5}}}{{\rm{H}}_{{\rm{12}}}}}}{{{\rm{8}}\;\abolish{{{\rm{mol}}\;{{\rm{O}}_{\rm{2}}}}}}}\;{\rm{ = }}\;{\rm{1}}{\rm{.5625}}\;{\rm{mol}}\]

\[{\rm{northward}}\left( {{{\rm{H}}_{\rm{2}}}{\rm{O}}} \right)\;{\rm{ = }}\;{\rm{two}}{\rm{.5 }}\cancel{{{\rm{mol}}\;{{\rm{O}}_{\rm{2}}}}}\;{\rm{ \times }}\;\frac{{{\rm{half-dozen}}\;{\rm{mol}}\;{{\rm{H}}_{\rm{ii}}}{\rm{O}}}}{{{\rm{viii}}\;\abolish{{{\rm{mol}}\;{{\rm{O}}_{\rm{2}}}}}}}\;{\rm{ = }}\;{\rm{1}}{\rm{.875}}\;{\rm{mol}}\]

For the third row :

\[{\rm{due north}}\left( {{{\rm{C}}_{\rm{5}}}{{\rm{H}}_{{\rm{12}}}}} \right)\;{\rm{ = }}\;{\rm{3 }}\cancel{{{\rm{mol}}\;{\rm{C}}{{\rm{O}}_{\rm{two}}}}}\;{\rm{ \times }}\;\frac{{{\rm{ane}}\;{\rm{mol}}\;{{\rm{C}}_{\rm{5}}}{{\rm{H}}_{{\rm{12}}}}}}{{{\rm{v}}\;\cancel{{{\rm{mol}}\;{\rm{C}}{{\rm{O}}_{\rm{2}}}}}}}\;{\rm{ = }}\;{\rm{0}}{\rm{.6}}\;{\rm{mol}}\]

\[{\rm{due north}}\left( {{{\rm{O}}_{\rm{2}}}} \right)\;{\rm{ = }}\;{\rm{iii }}\abolish{{{\rm{mol}}\;{\rm{C}}{{\rm{O}}_{\rm{2}}}}}\;{\rm{ \times }}\;\frac{{{\rm{8}}\;{\rm{mol}}\;{{\rm{O}}_{\rm{2}}}}}{{{\rm{5}}\;\cancel{{{\rm{mol}}\;{\rm{C}}{{\rm{O}}_{\rm{2}}}}}}}\;{\rm{ = }}\;{\rm{4}}{\rm{.viii}}\;{\rm{mol}}\]

\[{\rm{due north}}\left( {{{\rm{H}}_{\rm{2}}}{\rm{O}}} \correct)\;{\rm{ = }}\;{\rm{3 }}\cancel{{{\rm{mol}}\;{\rm{C}}{{\rm{O}}_{\rm{two}}}}}\;{\rm{ \times }}\;\frac{{{\rm{vi}}\;{\rm{mol}}\;{{\rm{H}}_{\rm{2}}}{\rm{O}}}}{{{\rm{5}}\;\cancel{{{\rm{mol}}\;{\rm{C}}{{\rm{O}}_{\rm{2}}}}}}}\;{\rm{ = }}\;{\rm{3}}{\rm{.6}}\;{\rm{mol}}\]

For the fourth row:

\[{\rm{n}}\left( {{{\rm{C}}_{\rm{5}}}{{\rm{H}}_{{\rm{12}}}}} \right)\;{\rm{ = }}\;{\rm{5}}{\rm{.iv }}\abolish{{{\rm{mol}}\;{{\rm{H}}_{\rm{2}}}{\rm{O}}}}\;{\rm{ \times }}\;\frac{{{\rm{1}}\;{\rm{mol}}\;{{\rm{C}}_{\rm{v}}}{{\rm{H}}_{{\rm{12}}}}}}{{{\rm{6}}\;\cancel{{{\rm{mol}}\;{{\rm{H}}_{\rm{2}}}{\rm{O}}}}}}\;{\rm{ = }}\;{\rm{0}}{\rm{.9}}\;{\rm{mol}}\]

\[{\rm{north}}\left( {{{\rm{O}}_{\rm{two}}}} \right)\;{\rm{ = }}\;{\rm{5}}{\rm{.four }}\abolish{{{\rm{mol}}\;{{\rm{H}}_{\rm{2}}}{\rm{O}}}}\;{\rm{ \times }}\;\frac{{{\rm{eight}}\;{\rm{mol}}\;{{\rm{O}}_{\rm{2}}}}}{{{\rm{6}}\;\abolish{{{\rm{mol}}\;{{\rm{H}}_{\rm{2}}}{\rm{O}}}}}}\;{\rm{ = }}\;{\rm{7}}{\rm{.2}}\;{\rm{mol}}\]

\[{\rm{n}}\left( {{\rm{C}}{{\rm{O}}_{\rm{ii}}}} \right)\;{\rm{ = }}\;{\rm{5}}{\rm{.4 }}\cancel{{{\rm{mol}}\;{{\rm{H}}_{\rm{2}}}{\rm{O}}}}\;{\rm{ \times }}\;\frac{{{\rm{v}}\;{\rm{mol}}\;{\rm{C}}{{\rm{O}}_{\rm{2}}}}}{{{\rm{6}}\;\cancel{{{\rm{mol}}\;{{\rm{H}}_{\rm{two}}}{\rm{O}}}}}}\;{\rm{ = }}\;{\rm{iv}}{\rm{.5}}\;{\rm{mol}}\]

3.

How many grams of CO_ii and H₂O are produced from the combustion of 220. 1000 of propane (C₃H₈)?

C₃H_viii(k) + 5O₂(yard) → 3CO₂(g) + 4H₂O(thou)

respond

Solution

The corporeality of production, for a given amount of reactant, is calculated based on their molar/stoichiometric ratio. Then, the first pace is to decide the moles of propane. The overall plan is:

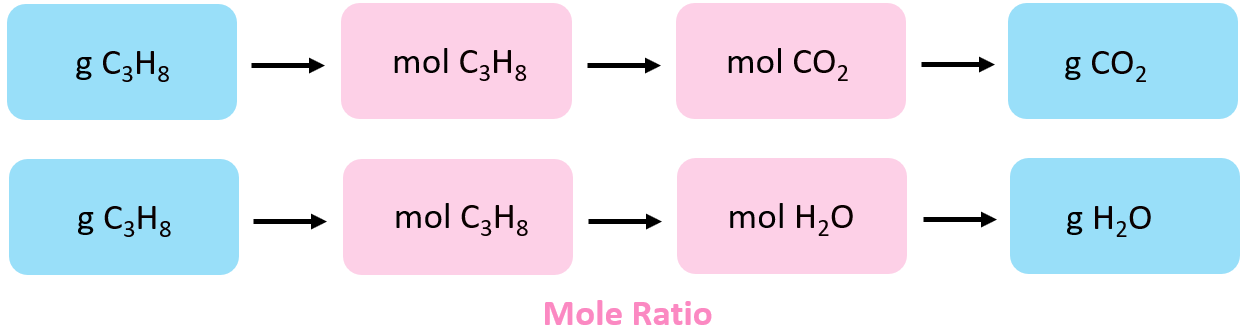
The moles of C₃H₈ are calculated using its molar mass:

\[{\rm{n(}}{{\rm{C}}_{\rm{3}}}{{\rm{H}}_{\rm{viii}}}{\rm{)}}\;{\rm{ = }}\;{\rm{220}}{\rm{.5}}\;{\rm{g}}\;{\rm{ \times }}\;\frac{{{\rm{1}}\;{\rm{mol}}}}{{{\rm{44}}{\rm{.1}}\;{\rm{g}}}}\;{\rm{ = }}\;{\rm{5}}{\rm{.00}}\;{\rm{mol}}\]

Next, we find the moles of CO₂ based on its molar ratio with C₃H_eight:

\[{\rm{n}}\left( {{\rm{C}}{{\rm{O}}_{\rm{2}}}} \correct)\;{\rm{ = }}\;{\rm{5}}{\rm{.00 }}\cancel{{{\rm{mol}}\;{{\rm{C}}_{\rm{3}}}{{\rm{H}}_{\rm{8}}}}}\;{\rm{ \times }}\;\frac{{{\rm{3}}\;{\rm{mol}}\;{\rm{C}}{{\rm{O}}_{\rm{2}}}}}{{{\rm{1}}\;\cancel{{{\rm{mol}}\;{{\rm{C}}_{\rm{3}}}{{\rm{H}}_{\rm{viii}}}}}}}\;{\rm{ = }}\;{\rm{15}}{\rm{.0}}\;{\rm{mol}}\]

And finally, the mass of the CO₂ is adamant using its moles and molar mass:

\[{\rm{thousand}}\left( {{\rm{C}}{{\rm{O}}_{\rm{2}}}} \right)\;{\rm{ = }}\;{\rm{15}}{\rm{.0 }}\cancel{{{\rm{mol}}\;}}\;{\rm{ \times }}\;\frac{{{\rm{44}}{\rm{.0}}\;{\rm{grand}}}}{{{\rm{1}}\;\abolish{{{\rm{mol}}\;}}}}\;{\rm{ = }}\;{\rm{660}}{\rm{.}}\;{\rm{chiliad}}\]

Follow the same procedure to detect the mass of H₂O:

\[{\rm{due north}}\left( {{{\rm{H}}_{\rm{two}}}{\rm{O}}} \right)\;{\rm{ = }}\;{\rm{5}}{\rm{.00 }}\abolish{{{\rm{mol}}\;{{\rm{C}}_{\rm{iii}}}{{\rm{H}}_{\rm{viii}}}}}\;{\rm{ \times }}\;\frac{{{\rm{4}}\;{\rm{mol}}\;{{\rm{H}}_{\rm{ii}}}{\rm{O}}}}{{{\rm{1}}\;\cancel{{{\rm{mol}}\;{{\rm{C}}_{\rm{iii}}}{{\rm{H}}_{\rm{8}}}}}}}\;{\rm{ = }}\;{\rm{xx}}{\rm{.0}}\;{\rm{mol}}\]

\[{\rm{m}}\left( {{{\rm{H}}_{\rm{ii}}}{\rm{O}}} \correct)\;{\rm{ = }}\;{\rm{20}}{\rm{.0 }}\abolish{{{\rm{mol}}\;}}\;{\rm{ \times }}\;\frac{{{\rm{18}}{\rm{.0}}\;{\rm{one thousand}}}}{{{\rm{ane}}\;\cancel{{{\rm{mol}}\;}}}}\;{\rm{ = }}\;{\rm{360}}{\rm{.}}\;{\rm{g}}\]

4.

How many grams of CaCl_two can be produced from 65.0 g of Ca(OH)₂ according to the following reaction,

Ca(OH)₂ + 2HCl → CaCl_ii + 2H_twoO

respond

97.3 g

Solution

Here is the conceptual program for solving this trouble:

The moles of Ca(OH)_two are calculated using its molar mass:

\[{\rm{due north}}\;{\rm{(Ca}}{\left( {{\rm{OH}}} \right)_{\rm{two}}}{\rm{)}}\;{\rm{ = }}\;{\rm{65}}{\rm{.0}}\;{\rm{g}}\;{\rm{ \times }}\;\frac{{{\rm{ane}}\;{\rm{mol}}}}{{{\rm{74}}{\rm{.i}}\;{\rm{g}}}}\;{\rm{ = }}\;{\rm{0}}{\rm{.877}}\;{\rm{mol}}\]

Next, nosotros find the moles of CaCl_ii based on its molar ratio with Ca(OH)₂:

\[{\rm{north}}\;\left( {{\rm{CaC}}{{\rm{l}}_{\rm{ii}}}} \correct)\;{\rm{ = }}\;{\rm{0}}{\rm{.877 }}\cancel{{{\rm{mol}}\;{\rm{Ca}}{{\left( {{\rm{OH}}} \right)}_{\rm{2}}}}}\;{\rm{ \times }}\;\frac{{{\rm{ane}}\;{\rm{mol}}\;{\rm{CaC}}{{\rm{l}}_{\rm{2}}}}}{{{\rm{1}}\;\cancel{{{\rm{mol}}\;{\rm{Ca}}{{\left( {{\rm{OH}}} \right)}_{\rm{2}}}}}}}\;{\rm{ = }}\;{\rm{0}}{\rm{.877}}\;{\rm{mol}}\]

Notice that moles of CaCl₂ are equal to the moles of Ca(OH)₂. This is considering of their 1:1 tooth ratio in the equation.

The terminal step is converting the moles to mass of the CaCl₂:

\[{\rm{one thousand}}\left( {{\rm{CaC}}{{\rm{50}}_{\rm{2}}}} \right)\;{\rm{ = }}\;{\rm{0}}{\rm{.877 }}\cancel{{{\rm{mol}}\;}}\;{\rm{ \times }}\;\frac{{{\rm{111}}\;{\rm{yard}}}}{{{\rm{1}}\;\abolish{{{\rm{mol}}\;}}}}\;{\rm{ = }}\;{\rm{97}}{\rm{.iii}}\;{\rm{thousand}}\]

This process can, and often is shown as a 1-step conversion every bit we practise in dimensional assay. Information technology would exist as follows:

\[{\rm{m}}\left( {{\rm{CaC}}{{\rm{l}}_{\rm{2}}}} \right)\;{\rm{ = }}\;{\rm{65}}{\rm{.0}}\;{\cancel{{{\rm{g}}\;{\rm{Ca}}{{\left( {{\rm{OH}}} \right)}_{\rm{2}}}}}_{\rm{\;}}}{\rm{ \times }}\;\frac{{{\rm{1}}\;\cancel{{{\rm{mol}}\;{\rm{Ca}}{{\left( {{\rm{OH}}} \right)}_{\rm{2}}}}}}}{{{\rm{74}}{\rm{.one}}\;\cancel{{{\rm{thousand}}\;{\rm{Ca}}{{\left( {{\rm{OH}}} \correct)}_{\rm{2}}}}}}}\;{\rm{ \times }}\;\frac{{{\rm{ane}}\;\cancel{{{\rm{mol}}\;{\rm{CaC}}{{\rm{fifty}}_{\rm{two}}}}}}}{{{\rm{1}}\;\abolish{{{\rm{mol}}\;{\rm{Ca}}{{\left( {{\rm{OH}}} \right)}_{\rm{2}}}}}}}\; \times \;\frac{{{\rm{111}}\;{\rm{g}}\;{\rm{CaC}}{{\rm{50}}_{\rm{2}}}}}{{{\rm{1}}\;\cancel{{{\rm{mol}}\;{\rm{CaC}}{{\rm{l}}_{\rm{2}}}\;}}}}\;\;{\rm{ = }}\;{\rm{97}}{\rm{.3}}\;{\rm{g}}\]

This method is completely fine, still, I prefer doing these conversions stepwise to ameliorate run across what happens in each pace, and therefore, almost exercises will exist solved by doing one conversion at a fourth dimension.

5.

How many moles of oxygen are formed when 75.0 g of Cu(NO₃)₂ decomposes according to the following reaction?

2Cu(NO_iii)₂→ 2CuO + 4NO₂ + O₂

answer

0.200 mol

Solution

The amount of product, for a given amount of reactant, is calculated based on their molar/stoichiometric ratio.

So, the conceptual plan is:

\[{\rm{n}}\;{\rm{(Cu}}{\left( {{\rm{Northward}}{{\rm{O}}_{\rm{3}}}} \correct)_{\rm{2}}}{\rm{\;)}}\;{\rm{ = }}\;{\rm{75}}{\rm{.0}}\;{\rm{g}}\;{\rm{ \times }}\;\frac{{{\rm{one}}\;{\rm{mol}}}}{{{\rm{187}}{\rm{.5}}\;{\rm{g}}}}\;{\rm{ = }}\;{\rm{0}}{\rm{.400}}\;{\rm{mol}}\]

\[{\rm{due north}}\;\left( {{{\rm{O}}_{{\rm{2\;}}}}} \right)\;{\rm{ = }}\;{\rm{0}}{\rm{.400}}\;\cancel{{{\rm{mol}}\;{\rm{Cu}}{{\left( {{\rm{N}}{{\rm{O}}_{\rm{3}}}} \correct)}_{\rm{2}}}{\rm{\;}}}}\;{\rm{ \times }}\;\frac{{{\rm{1}}\;{\rm{mol}}\;{{\rm{O}}_{\rm{two}}}}}{{\abolish{{{\rm{2}}\;{\rm{mol}}\;{\rm{Cu}}{{\left( {{\rm{North}}{{\rm{O}}_{\rm{three}}}} \right)}_{\rm{2}}}{\rm{\;}}}}}}\;{\rm{ = }}\;{\rm{0}}{\rm{.200}}\;{\rm{mol}}\]

6.

How many grams of MnCl₂can be prepared from 52.i grams of MnO₂?

MnO₂ + 4HCl → MnCl_ii+ Cl_ii + 2H₂O

answer

75.v one thousand

Solution

The amount of product, for a given amount of reactant, is calculated based on their tooth/stoichiometric ratio. So, the first step is to decide the moles of propane. The overall plan is:

The moles of MnO₂ are calculated using its molar mass:

\[{\rm{n}}\;{\rm{(Mn}}{{\rm{O}}_{\rm{ii}}}{\rm{)}}\;{\rm{ = }}\;{\rm{52}}{\rm{.1}}\;{\rm{one thousand}}\;{\rm{ \times }}\;\frac{{{\rm{i}}\;{\rm{mol}}}}{{{\rm{86}}{\rm{.9}}\;{\rm{g}}}}\;{\rm{ = }}\;{\rm{0}}{\rm{.600}}\;{\rm{mol}}\]

Next, we find the moles of MnCl₂ based on its molar ratio with MnO_ii:

\[{\rm{n}}\;\left( {{\rm{MnC}}{{\rm{l}}_{\rm{ii}}}} \right)\;{\rm{ = }}\;{\rm{0}}{\rm{.600 }}\cancel{{{\rm{mol}}\;{\rm{Mn}}{{\rm{O}}_{\rm{ii}}}}}\;{\rm{ \times }}\;\frac{{{\rm{ane}}\;{\rm{mol}}\;{\rm{MnC}}{{\rm{l}}_{\rm{ii}}}}}{{{\rm{1}}\;\cancel{{{\rm{mol}}\;{\rm{Mn}}{{\rm{O}}_{\rm{2}}}}}}}\;{\rm{ = }}\;{\rm{0}}{\rm{.600}}\;{\rm{mol}}\]

And finally, the mass of the MnCl₂ is determined using its moles and molar mass:

\[{\rm{g}}\left( {{\rm{MnC}}{{\rm{l}}_{\rm{2}}}} \right)\;{\rm{ = }}\;{\rm{0}}{\rm{.600 }}\cancel{{{\rm{mol}}\;}}\;{\rm{ \times }}\;\frac{{{\rm{125}}{\rm{.viii}}\;{\rm{g}}}}{{{\rm{1}}\;\cancel{{{\rm{mol}}\;}}}}\;{\rm{ = }}\;{\rm{75}}{\rm{.5g}}\]

7.

Determine the mass of oxygen that is formed when an 18.3-1000 sample of potassium chlorate is decomposed according to the following equation:

2KClO₃(s) → 2KCl(s) + 3O_ii(one thousand).

answer

7.xvi one thousand

Solution

The amount of product, for a given corporeality of reactant, is calculated based on their molar/stoichiometric ratio. And then, the first footstep is to decide the moles of propane. The conceptual plan is:

The moles of MnO₂ are calculated using its molar mass:

\[{\rm{n}}\;{\rm{(KCl}}{{\rm{O}}_{\rm{3}}}{\rm{)}}\;{\rm{ = }}\;{\rm{eighteen}}{\rm{.iii}}\;{\rm{chiliad}}\;{\rm{ \times }}\;\frac{{{\rm{1}}\;{\rm{mol}}}}{{{\rm{122}}{\rm{.6}}\;{\rm{g}}}}\;{\rm{ = }}\;{\rm{0}}{\rm{.149}}\;{\rm{mol}}\]

Next, we detect the moles of O₂ based on its molar ratio with KClO₃:

\[{\rm{n}}\;\left( {{{\rm{O}}_{\rm{2}}}} \correct)\;{\rm{ = }}\;{\rm{0}}{\rm{.149 }}\abolish{{{\rm{mol}}\;{\rm{KCl}}{{\rm{O}}_{\rm{3}}}}}\;{\rm{ \times }}\;\frac{{{\rm{3}}\;{\rm{mol}}\;{{\rm{O}}_{\rm{2}}}}}{{{\rm{two}}\;\abolish{{{\rm{mol}}\;{\rm{KCl}}{{\rm{O}}_{\rm{3}}}}}}}\;{\rm{ = }}\;{\rm{0}}{\rm{.224}}\;{\rm{mol}}\]

And finally, the mass of the MnCl_two is determined using its moles and molar mass:

\[{\rm{m}}\left( {{{\rm{O}}_{\rm{2}}}} \right)\;{\rm{ = }}\;{\rm{0}}{\rm{.224 }}\cancel{{{\rm{mol}}\;}}\;{\rm{ \times }}\;\frac{{{\rm{32}}{\rm{.0}}\;{\rm{grand}}}}{{{\rm{1}}\;\cancel{{{\rm{mol}}\;}}}}\;{\rm{ = }}\;{\rm{7}}{\rm{.16}}\;{\rm{m}}\]

8.

How many grams of H₂O will be formed when 48.0 grams H₂ are mixed with excess hydrogen gas?

2H₂ + O_two → 2H₂O

respond

432 one thousand

Solution

The amount of production, for a given amount of reactant, is calculated based on their molar/stoichiometric ratio. So, the offset step is to determine the moles of propane. The conceptual plan is:

The moles of H_iiO are calculated using its molar mass:

\[{\rm{n}}\;{\rm{(}}{{\rm{H}}_2}{\rm{)}}\;{\rm{ = }}\;{\rm{48}}{\rm{.0}}\;{\rm{g}}\;{\rm{ \times }}\;\frac{{{\rm{1}}\;{\rm{mol}}}}{{{\rm{2}}{\rm{.00}}\;{\rm{chiliad}}}}\;{\rm{ = }}\;{\rm{24}}{\rm{.0}}\;{\rm{mol}}\]

Next, we find the moles of H_twoO based on its molar ratio with H_two:

\[{\rm{n}}\;\left( {{{\rm{H}}_{\rm{2}}}{\rm{O}}} \right)\;{\rm{ = }}\;{\rm{24}}{\rm{.0 }}\cancel{{{\rm{mol}}\;{{\rm{H}}_{\rm{ii}}}}}\;{\rm{ \times }}\;\frac{{{\rm{ii}}\;{\rm{mol}}\;{{\rm{H}}_{\rm{2}}}{\rm{O}}}}{{{\rm{two}}\;\cancel{{{\rm{mol}}\;{{\rm{H}}_{\rm{2}}}}}}}\;{\rm{ = }}\;{\rm{24}}{\rm{.0}}\;{\rm{mol}}\]

And finally, the mass of the H₂O is determined using its moles and molar mass:

\[{\rm{m}}\left( {{{\rm{H}}_{\rm{2}}}{\rm{O}}} \right)\;{\rm{ = }}\;{\rm{24}}{\rm{.0 }}\cancel{{{\rm{mol}}\;}}\;{\rm{ \times }}\;\frac{{{\rm{eighteen}}{\rm{.0}}\;{\rm{m}}}}{{{\rm{i}}\;\cancel{{{\rm{mol}}\;}}}}\;{\rm{ = }}\;{\rm{432}}\;{\rm{g}}\]

9.

Consider the chlorination reaction of methane (CH4):

CH₄(g) + 4Cl₂(g) → CCl₄(g) + 4HCl(1000)

What mass of CCl_iv will be produced if 0.338 moles of CH₄ are used in the reaction?

reply

0.337 mol

Solution

The amount of production, for a given amount of reactant, is calculated based on their molar/stoichiometric ratio. And then, the starting time step is to decide the moles of propane. The conceptual program is:

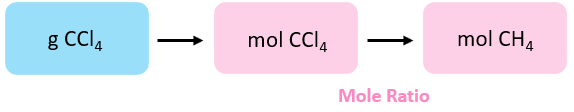
The moles of CCl₄ are calculated using its tooth mass:

\[{\rm{n}}\;{\rm{(CC}}{{\rm{l}}_{\rm{four}}}{\rm{)}}\;{\rm{ = }}\;{\rm{51}}{\rm{.9}}\;{\rm{g}}\;{\rm{ \times }}\;\frac{{{\rm{1}}\;{\rm{mol}}}}{{{\rm{153}}{\rm{.8}}\;{\rm{g}}}}\;{\rm{ = }}\;{\rm{0}}{\rm{.337}}\;{\rm{mol}}\]

Next, we find the moles of CH_iv based on its molar ratio with CCl_4.It is a 1:1 ratio, and then there is going to be 0.337 mol CH_four:

\[{\rm{n}}\;\left( {{\rm{C}}{{\rm{H}}_{\rm{iv}}}} \right)\;{\rm{ = }}\;{\rm{0}}{\rm{.337 }}\cancel{{{\rm{mol}}\;{\rm{CC}}{{\rm{l}}_{\rm{4}}}}}\;{\rm{ \times }}\;\frac{{{\rm{1}}\;{\rm{mol}}\;{\rm{C}}{{\rm{H}}_{\rm{4}}}}}{{{\rm{1}}\;\abolish{{{\rm{mol}}\;{\rm{CC}}{{\rm{l}}_{\rm{4}}}}}}}\;{\rm{ = }}\;{\rm{0}}{\rm{.337}}\;{\rm{mol}}\]

ten.

How many grams of Ba(NO₃)₂ can be produced by reacting 16.5 m of HNO_iii with an excess of Ba(OH)_ii?

answer

34.ii k

Solution

Nosotros need to first write the balanced chemical equation to do the calculations:

Ba(OH)_ii + 2HNO_iii → Ba(NO₃)₂ + 2H₂O

The conceptual programme would be:

So, let's first with the moles of HNO₃:

\[{\rm{n}}\;{\rm{(HN}}{{\rm{O}}_{\rm{3}}}{\rm{)}}\;{\rm{ = }}\;{\rm{16}}{\rm{.five}}\;{\rm{g}}\;{\rm{ \times }}\;\frac{{{\rm{i}}\;{\rm{mol}}}}{{{\rm{63}}{\rm{.0}}\;{\rm{g}}}}\;{\rm{ = }}\;{\rm{0}}{\rm{.262}}\;{\rm{mol}}\]

Once nosotros have the moles, we can determine the moles of Ba(NO₃)₂ based on the molar ratio, and then convert the moles to the mass:

\[{\rm{due north}}\;\left( {{\rm{Ba}}{{\left( {{\rm{N}}{{\rm{O}}_{\rm{3}}}} \correct)}_{\rm{2}}}} \correct)\;{\rm{ = }}\;{\rm{0}}{\rm{.262 }}\abolish{{{\rm{mol}}\;{\rm{HN}}{{\rm{O}}_{\rm{3}}}}}\;{\rm{ \times }}\;\frac{{{\rm{1}}\;{\rm{mol}}\;{\rm{Ba}}{{\left( {{\rm{Northward}}{{\rm{O}}_{\rm{3}}}} \right)}_{\rm{two}}}}}{{{\rm{2}}\;\cancel{{{\rm{mol}}\;{\rm{HN}}{{\rm{O}}_{\rm{3}}}}}}}\;{\rm{ = }}\;{\rm{0}}{\rm{.131}}\;{\rm{mol}}\]

\[{\rm{m}}\left( {{\rm{Ba}}{{\left( {{\rm{North}}{{\rm{O}}_{\rm{three}}}} \correct)}_{\rm{two}}}} \correct)\;{\rm{ = }}\;{\rm{0}}{\rm{.131 }}\cancel{{{\rm{mol}}\;}}\;{\rm{ \times }}\;\frac{{{\rm{261}}{\rm{.3}}\;{\rm{g}}}}{{{\rm{ane}}\;\cancel{{{\rm{mol}}\;}}}}\;{\rm{ = }}\;{\rm{34}}{\rm{.ii}}\;{\rm{g}}\]

11.

Ethanol tin exist obtained by fermentation – a complex chemical process breaking down glucose to ethanol and carbon dioxide.

                                                  C₆H₁₂O₆   →    2C₂H₅OH   +    2CO_two
glucose                   ethanol

How many mL of ethanol (d =0.789 g/mL) can be obtained by this process starting with 286 m of glucose?

answer

186 mL

Solution

This problem has an additional footstep of converting the mass of the production to book. Other than that, we follow the aforementioned strategy and steps as in the previous bug:

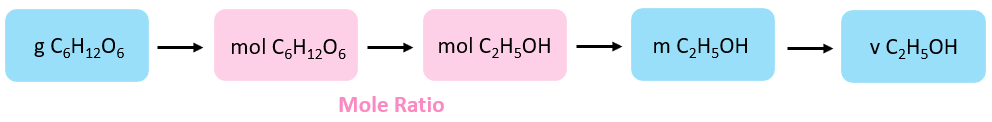
\[{\rm{north}}\;{\rm{(}}{{\rm{C}}_{\rm{vi}}}{{\rm{H}}_{{\rm{12}}}}{{\rm{O}}_{\rm{6}}}{\rm{)}}\;{\rm{ = }}\;{\rm{286}}\;{\rm{k}}\;{\rm{ \times }}\;\frac{{{\rm{1}}\;{\rm{mol}}}}{{{\rm{180}}{\rm{.2}}\;{\rm{k}}}}\;{\rm{ = }}\;{\rm{1}}{\rm{.59}}\;{\rm{mol}}\]

At present, nosotros can find the moles of C₂H₅OH:

\[{\rm{n}}\;\left( {{{\rm{C}}_{\rm{ii}}}{{\rm{H}}_{\rm{five}}}{\rm{OH}}} \correct)\;{\rm{ = }}\;{\rm{one}}{\rm{.59 }}\cancel{{{\rm{mol}}\;{{\rm{C}}_{\rm{6}}}{{\rm{H}}_{{\rm{12}}}}{{\rm{O}}_{\rm{half dozen}}}}}\;{\rm{ \times }}\;\frac{{{\rm{2}}\;{\rm{mol}}\;{{\rm{C}}_{\rm{two}}}{{\rm{H}}_{\rm{5}}}{\rm{OH}}}}{{{\rm{1}}\;\abolish{{{\rm{mol}}\;{{\rm{C}}_{\rm{half dozen}}}{{\rm{H}}_{{\rm{12}}}}{{\rm{O}}_{\rm{6}}}}}}}\;{\rm{ = }}\;{\rm{3}}{\rm{.eighteen}}\;{\rm{mol}}\]

\[{\rm{m}}\left( {{{\rm{C}}_{\rm{two}}}{{\rm{H}}_{\rm{5}}}{\rm{OH}}} \right)\;{\rm{ = }}\;{\rm{three}}{\rm{.18 }}\cancel{{{\rm{mol}}\;}}\;{\rm{ \times }}\;\frac{{{\rm{46}}{\rm{.i}}\;{\rm{g}}}}{{{\rm{1}}\;\cancel{{{\rm{mol}}\;}}}}\;{\rm{ = }}\;{\rm{147}}\;{\rm{g}}\]

The terminal step is converting the mass to volume:

\[{\rm{v}}\left( {{{\rm{C}}_{\rm{2}}}{{\rm{H}}_{\rm{five}}}{\rm{OH}}} \correct)\;{\rm{ = }}\;{\rm{147}}\;\abolish{{\rm{g}}}\;{\rm{ \times }}\;\frac{{{\rm{1}}\;{\rm{mL}}}}{{{\rm{0}}{\rm{.789}}\;\cancel{{\rm{g}}}}}\;{\rm{ = }}\;{\rm{186}}\;{\rm{mL}}\]

12.

36.0 1000 of butane (C₄H_ten) was burned in an excess of oxygen and the resulting carbon dioxide (CO_ii) was collected in a sealed vessel.

2C₄H₁₀ + 13O_two → 8CO₂ + 10H₂O

How many grams of LiOH will be necessary to consume all the CO₂ from the first reaction?

2LiOH + CO₂ → Li₂CO₃ + H₂O

answer

119 g

Solution

There are two reactions here, and the link betwixt them is the CO_two that is formed in the first reaction and used in the second.

So, the plan would be to decide the moles of CO₂ in the first reaction, and use information technology to calculate the moles, and consequently the mass of LiOH.

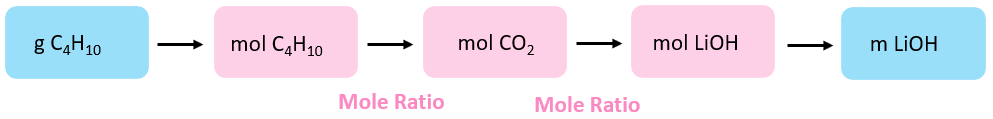
\[{\rm{n}}\;{\rm{(}}{{\rm{C}}_{\rm{iv}}}{{\rm{H}}_{{\rm{10}}}}{\rm{)}}\;{\rm{ = }}\;{\rm{36}}{\rm{.0}}\;{\rm{1000}}\;{\rm{ \times }}\;\frac{{{\rm{1}}\;{\rm{mol}}}}{{{\rm{58}}{\rm{.1}}\;{\rm{chiliad}}}}\;{\rm{ = }}\;{\rm{0}}{\rm{.620}}\;{\rm{mol}}\]

\[{\rm{n}}\;\left( {{\rm{C}}{{\rm{O}}_{\rm{2}}}} \right)\;{\rm{ = }}\;{\rm{0}}{\rm{.620 }}\cancel{{{\rm{mol}}\;{{\rm{C}}_{\rm{4}}}{{\rm{H}}_{{\rm{10}}}}}}\;{\rm{ \times }}\;\frac{{{\rm{8}}\;{\rm{mol}}\;{\rm{C}}{{\rm{O}}_{\rm{2}}}}}{{{\rm{2}}\cancel{{{\rm{mol}}\;{{\rm{C}}_{\rm{four}}}{{\rm{H}}_{{\rm{10}}}}}}}}\;{\rm{ = }}\;{\rm{2}}{\rm{.48}}\;{\rm{mol}}\]

This is the amount of CO_two that will exist reacted with LiOH in a ane:2 ratio. So, we can determine the moles of LiOH and convert them to the mass:

\[{\rm{northward}}\;\left( {{\rm{LiOH}}} \correct)\;{\rm{ = }}\;{\rm{ii}}{\rm{.48 }}\cancel{{{\rm{mol}}\;{\rm{C}}{{\rm{O}}_{\rm{2}}}}}\;{\rm{ \times }}\;\frac{{{\rm{ii}}\;{\rm{mol}}\;{\rm{LiOH}}}}{{{\rm{1}}\;\cancel{{{\rm{mol}}\;{\rm{C}}{{\rm{O}}_{\rm{2}}}}}}}\;{\rm{ = }}\;{\rm{4}}{\rm{.96}}\;{\rm{mol}}\]

\[{\rm{m}}\;\left( {{\rm{LiOH}}} \correct)\;{\rm{ = }}\;{\rm{4}}{\rm{.96}}\;\abolish{{{\rm{mol}}\;{\rm{LiOH}}}}\;{\rm{ \times }}\;\frac{{{\rm{24}}{\rm{.0}}\;{\rm{g}}\;{\rm{LiOH}}}}{{{\rm{one}}\;\abolish{{{\rm{mol}}\;{\rm{LiOH}}}}}}\;{\rm{ = }}\;{\rm{119}}\;{\rm{g}}\;\]

13.

Limiting Reactant

13. Which statement most limiting reactant is right?

a) The limiting reactant is the one in a smaller quantity.

b) The limiting reactant is the one in greater quantity.

c) The limiting reactant is the one producing less product.

d) The limiting reactant is the one producing more production.

answer

c) The limiting reactant is the ane producing less product than any of the other reactants.

14.

Find the limiting reactant for each initial amount of reactants.

4NH₃ + 5O₂ → 4NO + 6H₂O

a) 2 mol of NH_three and 2 mol of O₂

b) 2 mol of NH_iii and 3 mol of O₂

c) 3 mol of NH₃ and 3 mol of O_two

d) three mol of NH_iii and two mol of O_two

Notation: This is not a multiple-choice question. Each row represents a divide question where you demand to determine the limiting reactant.

answer

a) ii mol of NH₃ and two mol of O_two

b) 2 mol of NH₃ and 3 mol of O_ii

c) 3 mol of NH₃ and 3 mol of O₂

d) three mol of NH₃ and 2 mol of O₂

Solution

The limiting reactant is the one producing less product. So, to determine the limiting reactant for each pair, we need to option a product (NO or H_iiO) and meet whether NH₃ or O₂ will produce less product for the given mole ratio.

Let's do the calculations based on the corporeality of NO that can be formed.

a)

\[{\rm{north}}\;\left( {{\rm{NO}}} \right)\;{\rm{ = }}\;{\rm{2 }}\cancel{{{\rm{mol}}\;{\rm{Northward}}{{\rm{H}}_{\rm{iii}}}}}\;{\rm{ \times }}\;\frac{{{\rm{4}}\;{\rm{mol}}\;{\rm{NO}}}}{{{\rm{4}}\;\cancel{{{\rm{mol}}\;{\rm{Due north}}{{\rm{H}}_{\rm{3}}}}}}}\;{\rm{ = }}\;{\rm{2}}\;{\rm{mol}}\]

\[{\rm{n}}\;\left( {{\rm{NO}}} \right)\;{\rm{ = }}\;{\rm{ii }}\cancel{{{\rm{mol}}\;{{\rm{O}}_2}}}\;{\rm{ \times }}\;\frac{{{\rm{4}}\;{\rm{mol}}\;{\rm{NO}}}}{{{\rm{5}}\;\cancel{{{\rm{mol}}\;{{\rm{O}}_2}}}}}\;{\rm{ = }}\;{\rm{i}}{\rm{.6}}\;{\rm{mol}}\]

And so, for (a), O₂ is the limiting reactant.

b)

\[{\rm{n}}\;\left( {{\rm{NO}}} \right)\;{\rm{ = }}\;{\rm{2 }}\cancel{{{\rm{mol}}\;{\rm{North}}{{\rm{H}}_{\rm{3}}}}}\;{\rm{ \times }}\;\frac{{{\rm{4}}\;{\rm{mol}}\;{\rm{NO}}}}{{{\rm{iv}}\;\cancel{{{\rm{mol}}\;{\rm{N}}{{\rm{H}}_{\rm{iii}}}}}}}\;{\rm{ = }}\;{\rm{two}}\;{\rm{mol}}\]

\[{\rm{n}}\;\left( {{\rm{NO}}} \correct)\;{\rm{ = }}\;{\rm{3 }}\abolish{{{\rm{mol}}\;{{\rm{O}}_2}}}\;{\rm{ \times }}\;\frac{{{\rm{iv}}\;{\rm{mol}}\;{\rm{NO}}}}{{{\rm{5}}\;\cancel{{{\rm{mol}}\;{{\rm{O}}_2}}}}}\;{\rm{ = }}\;{\rm{2}}{\rm{.4}}\;{\rm{mol}}\]

So, for (b), NO is the limiting reactant.

c)

\[{\rm{northward}}\;\left( {{\rm{NO}}} \right)\;{\rm{ = }}\;{\rm{three }}\cancel{{{\rm{mol}}\;{\rm{Northward}}{{\rm{H}}_{\rm{3}}}}}\;{\rm{ \times }}\;\frac{{{\rm{4}}\;{\rm{mol}}\;{\rm{NO}}}}{{{\rm{4}}\;\abolish{{{\rm{mol}}\;{\rm{Due north}}{{\rm{H}}_{\rm{3}}}}}}}\;{\rm{ = }}\;{\rm{three}}\;{\rm{mol}}\]

\[{\rm{n}}\;\left( {{\rm{NO}}} \right)\;{\rm{ = }}\;{\rm{3 }}\cancel{{{\rm{mol}}\;{{\rm{O}}_2}}}\;{\rm{ \times }}\;\frac{{{\rm{four}}\;{\rm{mol}}\;{\rm{NO}}}}{{{\rm{v}}\;\abolish{{{\rm{mol}}\;{{\rm{O}}_2}}}}}\;{\rm{ = }}\;{\rm{two}}{\rm{.4}}\;{\rm{mol}}\]

So, for (c), O₂ is the limiting reactant.

d)

\[{\rm{n}}\;\left( {{\rm{NO}}} \right)\;{\rm{ = }}\;{\rm{3 }}\cancel{{{\rm{mol}}\;{\rm{N}}{{\rm{H}}_{\rm{3}}}}}\;{\rm{ \times }}\;\frac{{{\rm{iv}}\;{\rm{mol}}\;{\rm{NO}}}}{{{\rm{4}}\;\cancel{{{\rm{mol}}\;{\rm{Northward}}{{\rm{H}}_{\rm{iii}}}}}}}\;{\rm{ = }}\;{\rm{three}}\;{\rm{mol}}\]

\[{\rm{n}}\;\left( {{\rm{NO}}} \correct)\;{\rm{ = }}\;{\rm{two }}\cancel{{{\rm{mol}}\;{{\rm{O}}_2}}}\;{\rm{ \times }}\;\frac{{{\rm{four}}\;{\rm{mol}}\;{\rm{NO}}}}{{{\rm{5}}\;\cancel{{{\rm{mol}}\;{{\rm{O}}_2}}}}}\;{\rm{ = }}\;{\rm{1}}{\rm{.vi}}\;{\rm{mol}}\]

So, for (d), O₂ is the limiting reactant.

The shorter way of determining the limiting reactant is to divide the moles of a given reactant by its coefficient in the chemic reaction. This is the constructive quantity of the reactant as it takes into consideration not simply the amount of the reactant but as well its molar ratio in the reaction.

Let'south put the equation and the moles here and determine the LR past the ratio of the moles and coefficient:

4NH₃ + 5O₂ → 4NO + 6H₂O

a) 2 mol of NH_iii and 2 mol of O₂

b) two mol of NH₃ and iii mol of O_two

c) 3 mol of NH₃ and three mol of O_ii

d) iii mol of NH₃ and two mol of O₂

So, for (a), we are comparing 2/four mol of NH₃ with 2/five mol of O₂ , and therefore, O_ii is the LR.

For (b), we are comparing 2/4 mol of NH_iii with 3/5 mol of O₂ , and therefore, NH_three is the LR.

For (c), we are comparing three/4 mol of NH₃ with iii/5 mol of O₂ , and therefore, O₂ is the LR.

For (d),  3 mol of NH_three and 3/4 mol of NH ₃ with 2/5 mol of O₂, and therefore, O₂ is the LR.

15.

How many g of hydrogen are left over in producing ammonia when 14.0 thousand of nitrogen is reacted with viii.0 g of hydrogen?

N_ii(chiliad) + 3 H₂(grand) → two NH₃(grand)

answer

5.0 m

Solution

When the amounts of both reactants are given, you must determine the LR and then, based on the moles of the LR, determine the amount of production(s) that tin be formed. This is the standard procedure when working on examples covering limiting reactant.

Now, in this problem, we are not asked to determine the amount of whatever product, but rather we demand to determine how much hydrogen is left out in one case the reaction is complete. This already tells us that the nitrogen is the LR considering some of the hydrogen remains unreacted, then it must've been in excess.

The beginning step is, as always, to make up one's mind the moles of the reactants, then using the mole ratio, summate how much hydrogen has reacted. The remaining mass of the hydrogen is calculated by subtracting this amount from the initial mass.

\[{\rm{northward}}\;{\rm{(}}{{\rm{Northward}}_{\rm{two}}}{\rm{)}}\;{\rm{ = }}\;{\rm{14}}{\rm{.0}}\;{\rm{g}}\;{\rm{ \times }}\;\frac{{{\rm{1}}\;{\rm{mol}}}}{{{\rm{28}}{\rm{.0}}\;{\rm{g}}}}\;{\rm{ = }}\;{\rm{0}}{\rm{.500}}\;{\rm{mol}}\]

\[{\rm{north}}\;{\rm{(}}{{\rm{H}}_{\rm{two}}}{\rm{)}}\;{\rm{ = }}\;{\rm{8}}{\rm{.0}}\;{\rm{g}}\;{\rm{ \times }}\;\frac{{{\rm{1}}\;{\rm{mol}}}}{{{\rm{2}}{\rm{.0}}\;{\rm{chiliad}}}}\;{\rm{ = }}\;{\rm{4}}{\rm{.0}}\;{\rm{mol}}\]

The moles of hydrogen reacted are:

So, there are:

4.0 – 1.50 = ii.5 mol H_ii left out

\[{\rm{m}}\;{\rm{(}}{{\rm{H}}_{\rm{2}}}{\rm{)}}\;{\rm{ = }}\;{\rm{2}}{\rm{.5}}\;{\rm{mol}}\;{\rm{ \times }}\;\frac{{{\rm{2}}{\rm{.0}}\;{\rm{g}}}}{{{\rm{1}}\;{\rm{mol}}}}\;{\rm{ = }}\;{\rm{5}}{\rm{.0}}\;{\rm{g}}\]

16.

How many grams of PCl_iii volition be produced if 38.five g Cl₂ is reacted with 56.4 g P₄ according to the following equation?

6Cl₂(g) + P₄(s) → 4PCl_three(l)

answer

169 g

Solution

When the amounts of both reactants are given, yous must determine the LR and so, based on the moles of the LR, determine the amount of product(s) that can be formed.

The moles of Cl₂ and P₄ are:

\[{\rm{n}}\;{\rm{(C}}{{\rm{l}}_{\rm{2}}}{\rm{)}}\;{\rm{ = }}\;{\rm{38}}{\rm{.5}}\;{\rm{thousand}}\;{\rm{ \times }}\;\frac{{{\rm{one}}\;{\rm{mol}}}}{{{\rm{70}}{\rm{.9}}\;{\rm{g}}}}\;{\rm{ = }}\;{\rm{1}}{\rm{.84}}\;{\rm{mol}}\]

\[{\rm{n}}\;{\rm{(}}{{\rm{P}}_{\rm{4}}}{\rm{)}}\;{\rm{ = }}\;{\rm{56}}{\rm{.iv}}\;{\rm{g}}\;{\rm{ \times }}\;\frac{{{\rm{ane}}\;{\rm{mol}}}}{{{\rm{123}}{\rm{.9}}\;{\rm{thousand}}}}\;{\rm{ = }}\;{\rm{0}}{\rm{.455}}\;{\rm{mol}}\]

Next, nosotros calculate how much PCl₃ can be formed from each reactant:

\[{\rm{n}}\;\left( {{\rm{PC}}{{\rm{fifty}}_{\rm{three}}}} \right)\;{\rm{ = }}\;{\rm{1}}{\rm{.84 }}\cancel{{{\rm{mol}}\;{\rm{C}}{{\rm{50}}_{\rm{two}}}}}\;{\rm{ \times }}\;\frac{{{\rm{iv}}\;{\rm{mol}}\;{\rm{PC}}{{\rm{l}}_{\rm{three}}}}}{{{\rm{6}}\;\cancel{{{\rm{mol}}\;{\rm{C}}{{\rm{fifty}}_{\rm{2}}}}}}}\;{\rm{ = }}\;{\rm{1}}{\rm{.23}}\;{\rm{mol}}\]

\[{\rm{northward}}\;\left( {{\rm{PC}}{{\rm{fifty}}_{\rm{3}}}} \right)\;{\rm{ = }}\;{\rm{0}}{\rm{.455 }}\cancel{{{\rm{mol}}\;{{\rm{P}}_{\rm{iv}}}}}\;{\rm{ \times }}\;\frac{{{\rm{4}}\;{\rm{mol}}\;{\rm{PC}}{{\rm{fifty}}_{\rm{3}}}}}{{{\rm{1}}\;\cancel{{{\rm{mol}}\;{{\rm{P}}_{\rm{4}}}}}}}\;{\rm{ = }}\;{\rm{1}}{\rm{.82}}\;{\rm{mol}}\]

Cl_ii gives less PCl₃ and therefore, it is the LR and 1.23 mol of PCl_iii can be produced in this reaction.

The mass of PCl₃ is:

\[{\rm{m}}\;{\rm{(PC}}{{\rm{l}}_{\rm{3}}}{\rm{)}}\;{\rm{ = }}\;{\rm{1}}{\rm{.23}}\;{\rm{mol}}\;{\rm{ \times }}\;\frac{{{\rm{137}}{\rm{.3}}\;{\rm{g}}}}{{{\rm{1}}\;{\rm{mol}}}}\;{\rm{ = }}\;{\rm{169}}\;{\rm{grand}}\]

17.

How many grams of sulfur can be obtained if 12.half-dozen one thousand H_iiS is reacted with 14.6 g SO_two according to the following equation?

2H₂Southward(thou) + Then_two(thou) → 3S(s) + 2H_twoO(g)

answer

17.eight g

Solution

When the amount of both reactants is given, you must make up one's mind the LR then, based on the moles of the LR, make up one's mind the corporeality of production(south) that can be formed.

The moles of H_twoS and So_two are:

\[{\rm{due north}}\;{\rm{(}}{{\rm{H}}_{\rm{2}}}{\rm{Due south)}}\;{\rm{ = }}\;{\rm{12}}{\rm{.vi}}\;{\rm{g}}\;{\rm{ \times }}\;\frac{{{\rm{1}}\;{\rm{mol}}}}{{{\rm{34}}{\rm{.one}}\;{\rm{one thousand}}}}\;{\rm{ = }}\;{\rm{0}}{\rm{.370}}\;{\rm{mol}}\]

\[{\rm{northward}}\;{\rm{(S}}{{\rm{O}}_{\rm{2}}}{\rm{)}}\;{\rm{ = }}\;{\rm{14}}{\rm{.half-dozen}}\;{\rm{one thousand}}\;{\rm{ \times }}\;\frac{{{\rm{1}}\;{\rm{mol}}}}{{{\rm{64}}{\rm{.i}}\;{\rm{g}}}}\;{\rm{ = }}\;{\rm{0}}{\rm{.228}}\;{\rm{mol}}\]

Next, we calculate how much PCl₃ can exist formed from each reactant:

\[{\rm{n}}\;\left( {\rm{S}} \correct)\;{\rm{ = }}\;{\rm{0}}{\rm{.370 }}\cancel{{{\rm{mol}}\;{{\rm{H}}_{\rm{2}}}{\rm{S}}}}\;{\rm{ \times }}\;\frac{{{\rm{3}}\;{\rm{mol}}\;{\rm{S}}}}{{{\rm{2}}\;\abolish{{{\rm{mol}}\;{{\rm{H}}_{\rm{2}}}{\rm{S}}}}}}\;{\rm{ = }}\;{\rm{0}}{\rm{.555}}\;{\rm{mol}}\]

\[{\rm{n}}\;\left( {\rm{Southward}} \right)\;{\rm{ = }}\;{\rm{0}}{\rm{.228 }}\cancel{{{\rm{mol}}\;{\rm{S}}{{\rm{O}}_{\rm{2}}}}}\;{\rm{ \times }}\;\frac{{{\rm{3}}\;{\rm{mol}}\;{\rm{Due south}}}}{{{\rm{ane}}\;\abolish{{{\rm{mol}}\;{\rm{S}}{{\rm{O}}_{\rm{2}}}}}}}\;{\rm{ = }}\;{\rm{0}}{\rm{.684}}\;{\rm{mol}}\]

H_iiS gives less Due south and therefore, it is the LR and 0.555 mol of S can be produced in this reaction.

The mass of S is:

\[{\rm{m}}\;{\rm{(S)}}\;{\rm{ = }}\;{\rm{0}}{\rm{.555}}\;{\rm{mol}}\;{\rm{ \times }}\;\frac{{{\rm{32}}{\rm{.1}}\;{\rm{g}}}}{{{\rm{i}}\;{\rm{mol}}}}\;{\rm{ = }}\;{\rm{17}}{\rm{.eight}}\;{\rm{yard}}\]

18.

The post-obit equation represents the combustion of octane, C₈H₁₈, a component of gasoline:

2C₈H₁₈(yard) + 25O_two(g) → 16CO_ii(one thousand) + 18H₂O(yard)

Will 356 thou of oxygen be enough for the complete combustion of 954 g of octane?

answer

356 yard of oxygen is not enough for the complete combustion of 954 thou of octane.

Solution

First, calculate the moles of the reactants:

\[{\rm{n}}\;{\rm{(}}{{\rm{O}}_{\rm{ii}}}{\rm{)}}\;{\rm{ = }}\;{\rm{356}}\;{\rm{m}}\;{\rm{ \times }}\;\frac{{{\rm{one}}\;{\rm{mol}}}}{{{\rm{32}}{\rm{.0}}\;{\rm{g}}}}\;{\rm{ = }}\;{\rm{eleven}}{\rm{.4}}\;{\rm{mol}}\]

\[{\rm{n}}\;{\rm{(}}{{\rm{C}}_{\rm{8}}}{{\rm{H}}_{{\rm{18}}}}{\rm{)}}\;{\rm{ = }}\;{\rm{954}}\;{\rm{1000}}\;{\rm{ \times }}\;\frac{{{\rm{i}}\;{\rm{mol}}}}{{{\rm{114}}{\rm{.2}}\;{\rm{g}}}}\;{\rm{ = }}\;{\rm{viii}}{\rm{.35}}\;{\rm{mol}}\]

And now let'south see how many moles of O₂ are needed to react with 8.35 mol of C₈H₁₈:

\[{\rm{n}}\;\left( {{{\rm{O}}_{\rm{two}}}} \correct)\;{\rm{ = }}\;{\rm{eight}}{\rm{.35 }}\cancel{{{\rm{mol}}\;{{\rm{C}}_{\rm{8}}}{{\rm{H}}_{{\rm{18}}}}}}\;{\rm{ \times }}\;\frac{{{\rm{25}}\;{\rm{mol}}\;{{\rm{O}}_{\rm{2}}}}}{{{\rm{ii}}\;\abolish{{{\rm{mol}}\;{{\rm{C}}_{\rm{viii}}}{{\rm{H}}_{{\rm{18}}}}}}}}\;{\rm{ = }}\;{\rm{104}}\;{\rm{mol}}\]

104 moles of O_ii are needed to react with simply 8.35 mol of C₈H_eighteen and this is because of the 25:2 mole ratio. And then, 356 one thousand of oxygen is not plenty for the complete combustion of 954 k of octane.

xix.

When 140.0 g of AgNO_iii was added to an aqueous solution of NaCl, 86.0 g of AgCl was collected every bit a white precipitate. Which salt was the limiting reactant in this reaction? How many grams of NaCl were present in the solution when AgNO₃ was added?

AgNO₃(aq) + NaCl(aq) → AgCl(south) + NaNO_iii(aq)

answer

NaCl was the limiting reactant and 35.0 k of it were present in the solution when AgNO_threewas added.

Solution

We need to find the moles of AgCl which volition allow us to calculate how much AgNO₃ and NaCl had reacted in the reaction.

\[{\rm{n}}\;{\rm{(AgCl)}}\;{\rm{ = }}\;{\rm{86}}{\rm{.0}}\;{\rm{g}}\;{\rm{ \times }}\;\frac{{{\rm{1}}\;{\rm{mol}}}}{{{\rm{143}}{\rm{.3}}\;{\rm{yard}}}}\;{\rm{ = }}\;{\rm{0}}{\rm{.600}}\;{\rm{mol}}\]

The stoichiometric ratio of all the reactants and products is1:ane, and therefore, there were 0.600 mol of AgNO₃ and 0.600 mol of NaCl participating in the reaction.

Now, permit'south calculate the moles of 140.0 grand of AgNO_iii and see whether it corresponds to 0.600 mol. If it is more than than that, then AgNO_iii was added in backlog and NaCl must be the limiting reactant:

\[{\rm{n}}\;{\rm{(AgN}}{{\rm{O}}_{\rm{3}}}{\rm{)}}\;{\rm{ = }}\;{\rm{140}}{\rm{.0}}\;{\rm{g}}\;{\rm{ \times }}\;\frac{{{\rm{one}}\;{\rm{mol}}}}{{{\rm{169}}{\rm{.nine}}\;{\rm{m}}}}\;{\rm{ = }}\;{\rm{0}}{\rm{.824}}\;{\rm{mol}}\]

So, 0.824 mol of AgNO₃ were added to the solution, just only 0.600 mol had reacted which ways that is how much NaCl was nowadays in the solution, and it was not enough to react with all the AgNO_3.

And this confirms that AgNO₃ was added in backlog and NaCl is the limiting reactant.

In the terminal step, nosotros make up one's mind the mass of 0.600 mol NaCl that was in the solution when AgNO_three was added:

\[{\rm{thousand}}\;{\rm{(NaCl)}}\;{\rm{ = }}\;{\rm{0}}{\rm{.600}}\;{\rm{mol}}\;{\rm{ \times }}\;\frac{{{\rm{58}}{\rm{.4}}\;{\rm{thousand}}}}{{{\rm{1}}\;{\rm{mol}}}}\;{\rm{ = }}\;{\rm{35}}{\rm{.0}}\;{\rm{g}}\]

20.

Consider the reaction between MnO₂ and HCl:

MnO_two + 4HCl → MnCl_two + Cl_ii + 2H_iiO

What is the theoretical yield of MnCl₂ in grams when 165 m of MnO_two is added to a solution containing 94.2 g of HCl?

answer

0.645 mol or 81.1 one thousand MnCl₂

Solution

The theoretical yield is the amount of product that can be formed, so this problem is similar to the ones nosotros have been working on.

The amounts of both reactants are given, so we determine the LR and then, based on the moles of the LR, make up one's mind the amount of product(due south) that tin can exist formed.

The moles of MnO_two and HCl are:

\[{\rm{northward}}\;{\rm{(Mn}}{{\rm{O}}_{\rm{two}}}{\rm{)}}\;{\rm{ = }}\;{\rm{165}}\;{\rm{g}}\;{\rm{ \times }}\;\frac{{{\rm{one}}\;{\rm{mol}}}}{{{\rm{86}}{\rm{.ix}}\;{\rm{m}}}}\;{\rm{ = }}\;{\rm{1}}{\rm{.xc}}\;{\rm{mol}}\]

\[{\rm{n}}\;{\rm{(HCl)}}\;{\rm{ = }}\;{\rm{94}}{\rm{.ii}}\;{\rm{g}}\;{\rm{ \times }}\;\frac{{{\rm{1}}\;{\rm{mol}}}}{{{\rm{36}}{\rm{.5}}\;{\rm{k}}}}\;{\rm{ = }}\;{\rm{2}}{\rm{.58}}\;{\rm{mol}}\]

Adjacent, we calculate how much MnCl_ii tin can exist formed from each reactant:

\[{\rm{n}}\;\left( {{\rm{MnC}}{{\rm{fifty}}_{\rm{2}}}} \correct)\;{\rm{ = }}\;{\rm{1}}{\rm{.90 }}\cancel{{{\rm{mol}}\;{\rm{Mn}}{{\rm{O}}_{\rm{ii}}}}}\;{\rm{ \times }}\;\frac{{{\rm{i}}\;{\rm{mol}}\;{\rm{MnC}}{{\rm{fifty}}_{\rm{2}}}}}{{{\rm{1}}\;\cancel{{{\rm{mol}}\;{\rm{Mn}}{{\rm{O}}_{\rm{two}}}}}}}\;{\rm{ = }}\;{\rm{1}}{\rm{.90}}\;{\rm{mol}}\]

\[{\rm{north}}\;\left( {{\rm{MnC}}{{\rm{l}}_{\rm{2}}}} \right)\;{\rm{ = }}\;{\rm{ii}}{\rm{.58 }}\cancel{{{\rm{mol}}\;{\rm{HCl}}}}\;{\rm{ \times }}\;\frac{{{\rm{one}}\;{\rm{mol}}\;{\rm{MnC}}{{\rm{50}}_{\rm{two}}}}}{{{\rm{4}}\;\cancel{{{\rm{mol}}\;{\rm{HCl}}}}}}\;{\rm{ = }}\;{\rm{0}}{\rm{.645}}\;{\rm{mol}}\]

HCl gives less production so, information technology is the LR, and therefore, 0.645 mol MnCl₂ is the theoretical yield of the reaction.

If you are asked to find the theoretical yield in grams, then catechumen the moles to grams using the molar mass of MnCl_2:

\[{\rm{m}}\;{\rm{(MnC}}{{\rm{l}}_{\rm{2}}}{\rm{)}}\;{\rm{ = }}\;{\rm{0}}{\rm{.645}}\;{\rm{mol}}\;{\rm{ \times }}\;\frac{{{\rm{125}}{\rm{.eight}}\;{\rm{g}}}}{{{\rm{one}}\;{\rm{mol}}}}\;{\rm{ = }}\;{\rm{81}}{\rm{.1}}\;{\rm{chiliad}}\]

21.

Percent Yield

21. In a chemistry experiment, a student obtained 5.68 grand of a production. What is the pct yield of the product if the theoretical yield was 7.12 g?

answer

79.viii %

Solution

The percent yield of the reaction is the ratio of the actual over the theoretical yield. What we obtain is the actual yield and the maximum amount of product that can be obtained from the given corporeality of the limiting reactant is the theoretical yield.

Then, in this example, the actual yield is 5.68 one thousand, and the theoretical yield is 7.12 grand.

\[{\rm{\% }}\;{\rm{Yield}}\;{\rm{ = }}\;\frac{{\rm{A}}}{{\rm{T}}}\;{\rm{ = }}\;\frac{{{\rm{5}}{\rm{.68}}\;{\rm{thousand}}}}{{{\rm{7}}{\rm{.12}}\;{\rm{g}}}}\; \times \;100\% \; = \;79.8\;\% \]

22.

When 38.45 g CCl_iv is reacted with an excess of HF, 21.3 yard CCl₂F₂ is obtained. Summate the theoretical and percent yields of this reaction.

CCl_iv + 2HF → CCl₂F₂ + 2HCl

reply

70.five %

Solution

To notice the theoretical yield, we need to calculate the moles of CCl₄ and, using the mole ratio, make up one's mind how much CCl₂F₂ can be formed.

\[{\rm{northward}}\;{\rm{(CC}}{{\rm{50}}_{\rm{four}}}{\rm{)}}\;{\rm{ = }}\;{\rm{38}}{\rm{.45}}\;{\rm{thou}}\;{\rm{ \times }}\;\frac{{{\rm{1}}\;{\rm{mol}}}}{{{\rm{153}}{\rm{.8}}\;{\rm{g}}}}\;{\rm{ = }}\;{\rm{0}}{\rm{.250}}\;{\rm{mol}}\]

The amount of CCl₂F₂ that can be formed from this is likewise 0.250 mol considering of the 1:1 tooth ratio:

\[{\rm{northward}}\;\left( {{\rm{CC}}{{\rm{l}}_{\rm{2}}}{{\rm{F}}_{\rm{ii}}}} \right)\;{\rm{ = }}\;{\rm{0}}{\rm{.25 }}\abolish{{{\rm{mol}}\;{\rm{CC}}{{\rm{50}}_{\rm{four}}}}}\;{\rm{ \times }}\;\frac{{{\rm{ane}}\;{\rm{mol}}\;{\rm{CC}}{{\rm{l}}_{\rm{2}}}{{\rm{F}}_{\rm{2}}}}}{{{\rm{i}}\;\cancel{{{\rm{mol}}\;{\rm{CC}}{{\rm{fifty}}_{\rm{4}}}}}}}\;{\rm{ = }}\;{\rm{0}}{\rm{.25}}\;{\rm{mol}}\]

The mass, which is also the theoretical yield of CCl_twoF₂ is:

\[{\rm{thousand}}\;{\rm{(CC}}{{\rm{l}}_{\rm{2}}}{{\rm{F}}_{\rm{2}}}{\rm{)}}\;{\rm{ = }}\;{\rm{0}}{\rm{.250}}\;{\rm{mol}}\;{\rm{ \times }}\;\frac{{{\rm{120}}{\rm{.9}}\;{\rm{g}}}}{{{\rm{i}}\;{\rm{mol}}}}\;{\rm{ = }}\;{\rm{30}}{\rm{.2}}\;{\rm{g}}\]

The percent yield of the reaction is the ratio of the actual over the theoretical yield:

\[{\rm{\% }}\;{\rm{Yield}}\;{\rm{ = }}\;\frac{{\rm{A}}}{{\rm{T}}}\;{\rm{ = }}\;\frac{{{\rm{21}}{\rm{.three}}\;{\rm{chiliad}}}}{{{\rm{30}}{\rm{.ii}}\;{\rm{yard}}}}\; \times \;100\% \; = \;70.5\;\% \]

23.

Atomic number 26(III) oxide reacts with carbon monoxide according to the equation:

Iron₂O₃(s) + 3CO(chiliad) → 2Fe(s) + 3CO_two(g)

What is the pct yield of this reaction if 623 thou of iron oxide produces 341 g of iron?

answer

78.iv%

Solution

The actual yield of the reaction is given equally 341 g Fe so, to determine the percent yield, we need to get-go calculate the theoretical yield. This is the amount of Fe that can be formed if all the starting textile (in this case Fe₂O_iii) converts into a production according to the chemical equation.

Then, we are going to summate the moles of 623 g Fe₂O₃ and determine the moles and the mass of the atomic number 26 based on the stoichiometric ratio:

\[{\rm{due north}}\;{\rm{(F}}{{\rm{e}}_{\rm{2}}}{{\rm{O}}_{\rm{3}}}{\rm{)}}\;{\rm{ = }}\;{\rm{623}}\;{\rm{g}}\;{\rm{ \times }}\;\frac{{{\rm{one}}\;{\rm{mol}}}}{{{\rm{159}}{\rm{.7}}\;{\rm{g}}}}\;{\rm{ = }}\;{\rm{3}}{\rm{.xc}}\;{\rm{mol}}\]

The amount of Fethat tin can exist formed from this is calculated using the mole ratio of the oxide and iron:

\[{\rm{northward}}\;\left( {{\rm{Atomic number 26}}} \right)\;{\rm{ = }}\;{\rm{iii}}{\rm{.90 }}\cancel{{{\rm{mol}}\;{\rm{F}}{{\rm{e}}_{\rm{2}}}{{\rm{O}}_{\rm{iii}}}}}\;{\rm{ \times }}\;\frac{{{\rm{2}}\;{\rm{mol}}\;{\rm{Atomic number 26}}}}{{{\rm{i}}\;\abolish{{{\rm{mol}}\;{\rm{F}}{{\rm{e}}_{\rm{ii}}}{{\rm{O}}_{\rm{iii}}}}}}}\;{\rm{ = }}\;{\rm{seven}}{\rm{.80}}\;{\rm{mol}}\]

The mass, which is also the theoretical yield of Fe is:

\[{\rm{yard}}\;{\rm{(Fe)}}\;{\rm{ = }}\;{\rm{vii}}{\rm{.80}}\;{\rm{mol}}\;{\rm{ \times }}\;\frac{{{\rm{55}}{\rm{.viii}}\;{\rm{g}}}}{{{\rm{ane}}\;{\rm{mol}}}}\;{\rm{ = }}\;{\rm{435}}\;{\rm{g}}\]

The percent yield of the reaction is the ratio of the actual over the theoretical yield:

\[{\rm{\% }}\;{\rm{Yield}}\;{\rm{ = }}\;\frac{{\rm{A}}}{{\rm{T}}}\;{\rm{ = }}\;\frac{{{\rm{341}}\;{\rm{g}}}}{{{\rm{435}}\;{\rm{one thousand}}}}\; \times \;100\% \; = \;78.4\;\% \]

24.

Determine the percent yield of the reaction if 77.0 m of CO_ii are formed from burning 2.00 moles of C₅H₁₂ in 4.00 moles of O₂.

C_vH₁₂ + eight O₂ → 5CO₂ + 6H₂O

answer

70.0 %

Solution

When the corporeality of both reactants is given, you lot must determine the LR and then, based on the moles of the LR, determine the amount of product(s) that can be formed. This would be the theoretical yield of CO_ii.

At present, we are given the moles of the reactants, so we calculate how much CO₂ can each produce:

\[{\rm{n}}\;\left( {{\rm{C}}{{\rm{O}}_{\rm{2}}}} \right)\;{\rm{ = }}\;{\rm{ii}}{\rm{.00 }}\cancel{{{\rm{mol}}\;{{\rm{C}}_{\rm{v}}}{{\rm{H}}_{{\rm{12}}}}}}\;{\rm{ \times }}\;\frac{{{\rm{5}}\;{\rm{mol}}\;{\rm{C}}{{\rm{O}}_{\rm{2}}}}}{{{\rm{1}}\;\cancel{{{\rm{mol}}\;{{\rm{C}}_{\rm{5}}}{{\rm{H}}_{{\rm{12}}}}}}}}\;{\rm{ = }}\;{\rm{10}}{\rm{.0}}\;{\rm{mol}}\]

\[{\rm{n}}\;\left( {{\rm{C}}{{\rm{O}}_{\rm{two}}}} \correct)\;{\rm{ = }}\;{\rm{4}}{\rm{.00 }}\cancel{{{\rm{mol}}\;{{\rm{O}}_{\rm{2}}}}}\;{\rm{ \times }}\;\frac{{{\rm{five}}\;{\rm{mol}}\;{\rm{C}}{{\rm{O}}_{\rm{2}}}}}{{{\rm{viii}}\;\abolish{{{\rm{mol}}\;{{\rm{O}}_{\rm{two}}}}}}}\;{\rm{ = }}\;{\rm{two}}{\rm{.50}}\;{\rm{mol}}\]

Because oxygen gives less product, it is the LR, and therefore, ii.50 mol CO_ii could be formed in this reaction. This is the theoretical yield which is grams is:

\[{\rm{m}}\;{\rm{(C}}{{\rm{O}}_{\rm{ii}}}{\rm{)}}\;{\rm{ = }}\;{\rm{2}}{\rm{.50}}\;{\rm{mol}}\;{\rm{ \times }}\;\frac{{{\rm{44}}{\rm{.0}}\;{\rm{g}}}}{{{\rm{1}}\;{\rm{mol}}}}\;{\rm{ = }}\;{\rm{110}}{\rm{.}}\;{\rm{grand}}\]

The percent yield of the reaction is the ratio of the actual over the theoretical yield:

\[{\rm{\% }}\;{\rm{Yield}}\;{\rm{ = }}\;\frac{{\rm{A}}}{{\rm{T}}}\;{\rm{ = }}\;\frac{{{\rm{77}}{\rm{.0}}\;{\rm{g}}}}{{{\rm{110}}{\rm{.}}\;{\rm{thousand}}}}\; \times \;100\% \; = \;70.0\;\% \]

25.

The percentage yield for the following reaction was determined to exist 84%:

North₂(grand) + 2H_two(g) → N₂H_four(l)

How many grams of hydrazine (North_iiH₄) can exist produced when 38.36 chiliad of nitrogen reacts with six.68 g of hydrogen?

answer

36.8 g

Solution

The problem asks us to detect the actual yield of the reaction given that the per centum yield is lxxx%.

When the amounts of both reactants are given, y'all must make up one's mind the LR and and then, based on the moles of the LR, determine the corporeality of production(s) that can be formed. This would be the theoretical yield of hydrazine, and we tin can use it with the percentage yield to find the actual yield of the reaction.

\[{\rm{northward}}\;{\rm{(}}{{\rm{Northward}}_{\rm{ii}}}{\rm{)}}\;{\rm{ = }}\;{\rm{38}}{\rm{.36}}\;{\rm{g}}\;{\rm{ \times }}\;\frac{{{\rm{one}}\;{\rm{mol}}}}{{{\rm{28}}{\rm{.0}}\;{\rm{m}}}}\;{\rm{ = }}\;{\rm{1}}{\rm{.37}}\;{\rm{mol}}\]

\[{\rm{n}}\;{\rm{(}}{{\rm{H}}_{\rm{ii}}}{\rm{)}}\;{\rm{ = }}\;{\rm{half dozen}}{\rm{.68}}\;{\rm{grand}}\;{\rm{ \times }}\;\frac{{{\rm{one}}\;{\rm{mol}}}}{{{\rm{two}}{\rm{.00}}\;{\rm{chiliad}}}}\;{\rm{ = }}\;{\rm{3}}{\rm{.34}}\;{\rm{mol}}\]

At present, we are given the moles of the reactants, so we calculate how much N₂H_iv can each produce:

\[{\rm{n}}\;\left( {{{\rm{Northward}}_{\rm{2}}}{{\rm{H}}_{\rm{iv}}}} \right)\;{\rm{ = }}\;{\rm{ane}}{\rm{.37 }}\cancel{{{\rm{mol}}\;{{\rm{N}}_{\rm{two}}}}}\;{\rm{ \times }}\;\frac{{{\rm{1}}\;{\rm{mol}}\;{{\rm{N}}_{\rm{2}}}{{\rm{H}}_{\rm{4}}}}}{{{\rm{1}}\;\abolish{{{\rm{mol}}\;{{\rm{N}}_{\rm{2}}}}}}}\;{\rm{ = }}\;{\rm{ane}}{\rm{.37}}\;{\rm{mol}}\]

\[{\rm{north}}\;\left( {{{\rm{N}}_{\rm{2}}}{{\rm{H}}_{\rm{4}}}} \correct)\;{\rm{ = }}\;{\rm{3}}{\rm{.34 }}\cancel{{{\rm{mol}}\;{{\rm{H}}_{\rm{2}}}}}\;{\rm{ \times }}\;\frac{{{\rm{1}}\;{\rm{mol}}\;{{\rm{N}}_{\rm{2}}}{{\rm{H}}_{\rm{four}}}}}{{{\rm{ii}}\;\cancel{{{\rm{mol}}\;{{\rm{H}}_{\rm{2}}}}}}}\;{\rm{ = }}\;{\rm{i}}{\rm{.67}}\;{\rm{mol}}\]

Northward_two gives less hydrazine and so, it is the LR, and therefore the theoretical yield of N₂H_four is 1.37 mol. The mass of Due north₂H₄ is:

\[{\rm{one thousand}}\;{\rm{(}}{{\rm{N}}_{\rm{2}}}{{\rm{H}}_{\rm{four}}}_{\rm{2}}{\rm{)}}\;{\rm{ = }}\;{\rm{1}}{\rm{.37}}\;{\rm{mol}}\;{\rm{ \times }}\;\frac{{{\rm{32}}{\rm{.0}}\;{\rm{chiliad}}}}{{{\rm{one}}\;{\rm{mol}}}}\;{\rm{ = }}\;{\rm{43}}{\rm{.8}}\;{\rm{m}}\]

The percent yield of the reaction is the ratio of the actual over the theoretical yield, and then rearranging this equation we can summate the actual yield:

\[{\rm{\% }}\;{\rm{Yield}}\;{\rm{ = }}\;\frac{{\rm{A}}}{{\rm{T}}}\;\]

A = T 10 % Yield

A = 43.8 x 0.84 = 36.viii thou

Some other approach for determining the actual yield is to convert the moles of limiting reactant to the percentage of the percent yield. And then, if the yield is 84%, we could have multiplied the moles of N_ii by 0.84 and determine the mass of N_twoH_iv based on that.

Nosotros would have 1.37 mole x 0.84 = 1.1508 mol N₂ which is the moles of nitrogen that actually convert into hydrazine. By the mole ratio, the moles of N₂H₄ would exist:

\[{\rm{n}}\;\left( {{{\rm{N}}_{\rm{2}}}{{\rm{H}}_{\rm{4}}}} \correct)\;{\rm{ = }}\;{\rm{i}}{\rm{.1508 }}\abolish{{{\rm{mol}}\;{{\rm{N}}_{\rm{2}}}}}\;{\rm{ \times }}\;\frac{{{\rm{1}}\;{\rm{mol}}\;{{\rm{Due north}}_{\rm{two}}}{{\rm{H}}_{\rm{iv}}}}}{{{\rm{one}}\;\cancel{{{\rm{mol}}\;{{\rm{N}}_{\rm{two}}}}}}}\;{\rm{ = }}\;{\rm{one}}{\rm{.1508}}\;{\rm{mol}}\]

And the mass would be:

\[{\rm{m}}\;{\rm{(}}{{\rm{Due north}}_{\rm{2}}}{{\rm{H}}_{\rm{four}}}_{\rm{2}}{\rm{)}}\;{\rm{ = }}\;{\rm{1}}{\rm{.1508}}\;{\rm{mol}}\;{\rm{ \times }}\;\frac{{{\rm{32}}{\rm{.0}}\;{\rm{1000}}}}{{{\rm{i}}\;{\rm{mol}}}}\;{\rm{ = }}\;{\rm{36}}{\rm{.8}}\;{\rm{k}}\]

26.

Silver metallic can exist prepared by reducing its nitrate, AgNO₃ with copper co-ordinate to the post-obit equation:

Cu(due south) + 2AgNO₃(aq) → Cu(NO₃)_two(aq) + 2Ag(southward)

What is the pct yield of the reaction if 71.v grams of Ag was obtained from 132.5 grams of AgNO₃?

answer

85%

Solution

The actual yield of the reaction is given as 71.5 g Ag so, to determine the percent yield, we demand to first calculate the theoretical yield. This is the amount of Ag that can exist formed if all the starting cloth (in this example AgNO₃) converts into product according to the chemical equation.

So, we are going to calculate the moles of 132.5 one thousand AgNO₃ and determine the moles and the mass of the silver based on their stoichiometric ratio:

\[{\rm{n}}\;{\rm{(AgN}}{{\rm{O}}_{\rm{3}}}{\rm{)}}\;{\rm{ = }}\;{\rm{132}}{\rm{.five}}\;{\rm{thou}}\;{\rm{ \times }}\;\frac{{{\rm{i}}\;{\rm{mol}}}}{{{\rm{169}}{\rm{.9}}\;{\rm{g}}}}\;{\rm{ = }}\;{\rm{0}}{\rm{.780}}\;{\rm{mol}}\]

\[{\rm{north}}\;\left( {{\rm{Ag}}} \correct)\;{\rm{ = }}\;{\rm{0}}{\rm{.780 }}\cancel{{{\rm{mol}}\;{\rm{AgN}}{{\rm{O}}_{\rm{3}}}}}\;{\rm{ \times }}\;\frac{{{\rm{2}}\;{\rm{mol}}\;{\rm{Ag}}}}{{{\rm{two}}\;\abolish{{{\rm{mol}}\;{\rm{AgN}}{{\rm{O}}_{\rm{3}}}}}}}\;{\rm{ = }}\;{\rm{0}}{\rm{.780}}\;{\rm{mol}}\]

The mass, which is also the theoretical yield of Ag is:

\[{\rm{thousand}}\;{\rm{(Ag)}}\;{\rm{ = }}\;{\rm{0}}{\rm{.780}}\;{\rm{mol}}\;{\rm{ \times }}\;\frac{{{\rm{107}}{\rm{.nine}}\;{\rm{g}}}}{{{\rm{1}}\;{\rm{mol}}}}\;{\rm{ = }}\;{\rm{84}}{\rm{.2}}\;{\rm{m}}\]

The percent yield of the reaction is the ratio of the actual over the theoretical yield:

\[{\rm{\% }}\;{\rm{Yield}}\;{\rm{ = }}\;\frac{{\rm{A}}}{{\rm{T}}}\;{\rm{ = }}\;\frac{{{\rm{71}}{\rm{.5}}\;{\rm{thousand}}}}{{{\rm{84}}{\rm{.2}}\;{\rm{one thousand}}}}\; \times \;100\% \; = \;85\;\% \]

27.

Industrially, nitric acid is produced from ammonia by the Ostwald process in a series of reactions:

4NH₃(g) + 5O₂(g) → 4NO(g) + 6H_twoO(l)

2NO(g) + O_ii(grand) → 2NO₂(g)

2NO₂(g) + H₂O(fifty) → HNO₃(aq) + HNO_two(aq)

Considering that each reaction has an 85% percent yield, how many grams of NH₃ must be used to produce 25.0 kg of HNO₃ by the above procedure?

answer

2.xx 10 10⁴ grand

Solution

Because we are given the mass of the product and need to determine the mass of the starting material, the calculations are going to exist in reverse gild. So, first, nosotros can calculate the moles of HNO_three and using the mole ratio, discover the moles of NO₂ which is the link between the 3^rd and 2^nd reactions.

Earlier using the mass of HNO₃, catechumen it to grams because the molar mass is given in grams per mole:

\[{\rm{m}}\left( {{\rm{HN}}{{\rm{O}}_{\rm{3}}}} \right)\;{\rm{ = }}\;{\rm{25}}{\rm{.0}}\;\cancel{{{\rm{kg}}}}\;{\rm{ \times }}\;\frac{{{\rm{1000}}\;{\rm{g}}}}{{{\rm{1}}\;\abolish{{{\rm{kg}}}}}}\;{\rm{ = }}\;{\rm{2}}{\rm{.5}}\;{\rm{ \times }}\;{\rm{ane}}{{\rm{0}}^{\rm{4}}}\;{\rm{g}}\]

\[{\rm{north}}\;{\rm{(HN}}{{\rm{O}}_{\rm{iii}}}{\rm{)}}\;{\rm{ = }}\;{\rm{2}}{\rm{.fifty}}\;{\rm{ \times }}\;{10^4}\;{\rm{yard}}\;{\rm{ \times }}\;\frac{{{\rm{one}}\;{\rm{mol}}}}{{{\rm{63}}{\rm{.0}}\;{\rm{g}}}}\;{\rm{ = }}\;{\rm{397}}\;{\rm{mol}}\]

\[{\rm{n}}\;\left( {{\rm{N}}{{\rm{O}}_{\rm{2}}}} \right)\;{\rm{ = }}\;{\rm{397 }}\cancel{{{\rm{mol}}\;{\rm{HN}}{{\rm{O}}_{\rm{3}}}}}\;{\rm{ \times }}\;\frac{{{\rm{2}}\;{\rm{mol}}\;{\rm{N}}{{\rm{O}}_{\rm{ii}}}}}{{{\rm{i}}\;\abolish{{{\rm{mol}}\;{\rm{HN}}{{\rm{O}}_{\rm{3}}}}}}}\;{\rm{ = }}\;{\rm{794}}\;{\rm{mol}}\]

Now, this would have been the conversion if it was a process with a 100% yield. However, considering each step of this procedure has an 85% percentage yield, we need to multiply each mole conversion past a factor of

\[\frac{{{\rm{100\% }}}}{{{\rm{85\% }}}}\;{\rm{or}}\;{\rm{simply}}\;\frac{{{\rm{100}}}}{{{\rm{85}}}}\]

And then, the moles of NO₂ that produced 397 mol of HNO_iii would be:

\[{\rm{northward}}\;\left( {{\rm{N}}{{\rm{O}}_{\rm{ii}}}} \correct)\;{\rm{ = }}\;{\rm{794}}\;{\rm{mol}}\;{\rm{ \times }}\;\frac{{{\rm{100}}}}{{{\rm{85}}}}\;{\rm{ = }}\;{\rm{934}}\;{\rm{mol}}\]

Now, we go to the second reaction and see how much NO was needed to produce 934 mol NO_two because that the yield of the reaction is again 85%.

2NO(one thousand) + O₂(yard) → 2NO_two(yard)

\[{\rm{northward}}\;\left( {{\rm{NO}}} \right)\;{\rm{ = }}\;{\rm{934 }}\cancel{{{\rm{mol}}\;{\rm{North}}{{\rm{O}}_{\rm{ii}}}}}\;{\rm{ \times }}\;\frac{{{\rm{two}}\;{\rm{mol}}\;{\rm{NO}}}}{{{\rm{ii}}\;\cancel{{{\rm{mol}}\;{\rm{N}}{{\rm{O}}_{\rm{2}}}}}}}\; \times \;\frac{{100}}{{85}}\;{\rm{ = }}\;{\rm{1098}}\;{\rm{mol}}\]

Side by side, we do the same for the first reaction and determine how much NH₃ was needed to produce 1098 mol NO considering that the yield of the reaction is again 85%.

4NH₃(g) + 5O₂(g) → 4NO(one thousand) + 6H_iiO(fifty)

\[{\rm{n}}\;\left( {{\rm{N}}{{\rm{H}}_{\rm{iii}}}} \right)\;{\rm{ = }}\;{\rm{1098 }}\cancel{{{\rm{mol}}\;{\rm{NO}}}}\;{\rm{ \times }}\;\frac{{{\rm{4}}\;{\rm{mol}}\;{\rm{N}}{{\rm{H}}_{\rm{iii}}}}}{{{\rm{4}}\;\cancel{{{\rm{mol}}\;{\rm{NO}}}}}}\;{\rm{ \times }}\;\frac{{{\rm{100}}}}{{{\rm{85}}}}\;{\rm{ = }}\;{\rm{1293}}\;{\rm{mol}}\]

In the final step, we convert the moles to the mass of ammonia:

\[{\rm{m}}\;{\rm{(N}}{{\rm{H}}_{\rm{3}}}{\rm{)}}\;{\rm{ = }}\;{\rm{1293}}\;{\rm{mol}}\;{\rm{ \times }}\;\frac{{{\rm{17}}{\rm{.0}}\;{\rm{thou}}}}{{{\rm{1}}\;{\rm{mol}}}}\;{\rm{ = }}\;{\rm{21,981}}\;{\rm{g}}\]

Rounding off to three meaning figures, nosotros get:

2.20 x x^four g

28.

Aspirin (acetyl salicylic acid) is widely used to treat pain, fever, and inflammation. It is produced from the reaction of salicylic acid with acerb anhydride. The chemical equation for aspirin synthesis is shown below:

In one container, 10.00 kg of salicylic acrid is mixed with 10.00 kg of acerb anhydride.

a) Which reactant is limiting? Which is in excess?
b) What mass of backlog reactant is left over?
c) What mass of aspirin is formed assuming 100% yield (Theoretical yield)?
d) What mass of aspirin is formed if the reaction yield is 70.0% ?
e) If the actual yield of aspirin is 11.2 kg, what is the percent yield?
f) How many kg of salicylic acrid is needed to produce 20.0 kg of aspirin if the reaction yield is 85.0% ?

a)

respond

Salicylic acid is the limiting reagent

b)

answer

2.608 x 10³ g Acetic anhydride

c)

answer

1.305 x ten⁴ thousand Aspirin

d)

answer

9.14 x 10³ thousand Aspirin

e)

answer

85.viii %

f)

answer

18.one kg

Solution

a)Which reactant is limiting? Which is in excess?

The limiting reactant is the one producing less production, then nosotros need to calculate the moles of 00 kg salicylic acid and x.00 kg acerb anhydride and meet which 1 produces less aspirin. Because the mole ratio of all the reactants and products is 1:1, whichever has a smaller number of moles, it is the limiting reactant.

Earlier using the masses, catechumen them to grams because the tooth mass is given in grams per mole:

\[{\rm{m}}\left( {{\rm{salicylic acid}}} \right)\;{\rm{ = }}\;{\rm{10}}{\rm{.00}}\;\cancel{{{\rm{kg}}}}\;{\rm{ \times }}\;\frac{{{\rm{1000}}\;{\rm{g}}}}{{{\rm{1}}\;\cancel{{{\rm{kg}}}}}}\;{\rm{ = }}\;{\rm{i}}{\rm{.000}}\;{\rm{ \times }}\;{\rm{i}}{{\rm{0}}^{\rm{4}}}\;{\rm{g}}\]

\[{\rm{k}}\left( {{\rm{acetic anhydride}}} \right)\;{\rm{ = }}\;{\rm{x}}{\rm{.00}}\;\abolish{{{\rm{kg}}}}\;{\rm{ \times }}\;\frac{{{\rm{1000}}\;{\rm{g}}}}{{{\rm{1}}\;\abolish{{{\rm{kg}}}}}}\;{\rm{ = }}\;{\rm{1}}{\rm{.000}}\;{\rm{ \times }}\;{\rm{one}}{{\rm{0}}^{\rm{4}}}\;{\rm{g}}\]

\[{\rm{north}}\;{\rm{(salicylic acid)}}\;{\rm{ = }}\;{\rm{one}}{\rm{.000}}\;{\rm{ \times }}\;{\rm{1}}{{\rm{0}}^{\rm{4}}}\;{\rm{one thousand}}\;{\rm{ \times }}\;\frac{{{\rm{ane}}\;{\rm{mol}}}}{{{\rm{138}}{\rm{.1}}\;{\rm{grand}}}}\;{\rm{ = }}\;{\rm{72}}{\rm{.4}}\;{\rm{mol}}\]

\[{\rm{due north}}\;{\rm{(acerb anhydride)}}\;{\rm{ = }}\;{\rm{1}}{\rm{.000}}\;{\rm{ \times }}\;{\rm{1}}{{\rm{0}}^{\rm{4}}}\;{\rm{one thousand}}\;{\rm{ \times }}\;\frac{{{\rm{1}}\;{\rm{mol}}}}{{{\rm{102}}{\rm{.1}}\;{\rm{thousand}}}}\;{\rm{ = }}\;{\rm{97}}{\rm{.9}}\;{\rm{mol}}\]

Salicylic acid is present in a smaller quantity, and because of the 1:i molar ratio of all the reactants and products, it is going to produce less aspirin, and therefore, it is the limiting reactant.

b) What mass of excess reactant is left over?

We know that salicylic acid is the limiting reactant, so the calculations are going to be based on its moles (72.4 mol). Using the mole ratio, we can calculate how much acetic anhydride has reacted. The remaining mass of the acetic anhydride is calculated by subtracting this corporeality from the initial mass.

Again, because of the one:1 molar ratio, there is going to be 72.4 mol acetic anhydride reacted:

\[{\rm{n}}\;\left( {{\rm{acetic anhydride}}} \correct)\;{\rm{ = }}\;{\rm{72}}{\rm{.4 }}\cancel{{{\rm{mol}}\;{\rm{salicylic acid}}}}\;{\rm{ \times }}\;\frac{{{\rm{1}}\;{\rm{mol}}\;{\rm{acetic anhydride}}}}{{{\rm{1}}\;\cancel{{{\rm{mol}}\;{\rm{salicylic acrid}}}}}}\;{\rm{ = }}\;{\rm{72}}{\rm{.4}}\;{\rm{mol}}\]

This corresponds to:

\[{\rm{chiliad}}\;{\rm{(acetic anhydride)}}\;{\rm{ = }}\;{\rm{72}}{\rm{.4}}\;{\rm{mol}}\;{\rm{ \times }}\;\frac{{{\rm{102}}{\rm{.i}}\;{\rm{g}}\;}}{{{\rm{1}}\;{\rm{mol}}}}\;{\rm{ = }}\;{\rm{7392}}\;{\rm{one thousand}}\]

The remaining mass of acetic anhydride is:

10,000 – 7392 = 2608 g = ii.608 kg

c) What mass of aspirin is formed assuming 100% yield (Theoretical yield)?

72.iv mol aspirin will exist formed considering of the ane:i molar ratio:

\[{\rm{n}}\;\left( {{\rm{aspirin}}} \right)\;{\rm{ = }}\;{\rm{72}}{\rm{.4 }}\cancel{{{\rm{mol}}\;{\rm{salicylic acrid}}}}\;{\rm{ \times }}\;\frac{{{\rm{one}}\;{\rm{mol}}\;{\rm{aspirin}}}}{{{\rm{1}}\;\abolish{{{\rm{mol}}\;{\rm{salicylic acid}}}}}}\;{\rm{ = }}\;{\rm{72}}{\rm{.4}}\;{\rm{mol}}\]

Using the molar mass of aspirin, we tin summate its mass for 100%-yield reaction:

\[{\rm{m}}\;{\rm{(aspirin)}}\;{\rm{ = }}\;{\rm{72}}{\rm{.4}}\;{\rm{mol}}\;{\rm{ \times }}\;\frac{{{\rm{180}}{\rm{.2}}\;{\rm{k}}}}{{{\rm{ane}}\;{\rm{mol}}}}\;{\rm{ = }}\;{\rm{xiii,046}}\;{\rm{g}}\]

This corresponds to 13.05 kg when divided by 1000.

d) What mass of aspirin is formed if the reaction yield is 70.0%?

To find the mass of aspirin when the percent yield is 70.0%, nosotros need to multiply the theoretical yield (13.05 kg) by 0.700:

1000 (aspirin) = 13.05 kg 10 0.700 = 9.14 kg

e) If the actual yield of aspirin is 11.2 kg, what is the percentage yield?

The percent yield of the reaction is the ratio of the bodily over the theoretical yield:

\[{\rm{\% }}\;{\rm{Yield}}\;{\rm{ = }}\;\frac{{\rm{A}}}{{\rm{T}}}\;{\rm{ = }}\;\frac{{{\rm{xi}}{\rm{.2}}\;{\rm{kg}}}}{{{\rm{13}}{\rm{.05}}\;{\rm{kg}}}}\;{\rm{ \times }}\;{\rm{100\% }}\;{\rm{ = }}\;{\rm{85}}{\rm{.8}}\;{\rm{\% }}\]

f) How many kg of salicylic acid is needed to produce 20.0 kg of aspirin if the reaction yield is 85.0% ?

Offset, calculate the moles of 20.0 kg aspirin which is 2.00 ten 10^four g:

\[{\rm{north}}\;{\rm{(aspirin)}}\;{\rm{ = }}\;{\rm{two}}{\rm{.0}}\;{\rm{ \times }}\;{\rm{one}}{{\rm{0}}^{\rm{four}}}\;{\rm{one thousand}}\;{\rm{ \times }}\;\frac{{{\rm{one}}\;{\rm{mol}}}}{{{\rm{180}}{\rm{.2}}\;{\rm{g}}}}\;{\rm{ = }}\;{\rm{111}}\;{\rm{mol}}\]

According to the mole ratio of the chemic equation, this is how much salicylic acid would exist needed because of the 1:ane mole ratio.

However, considering the reaction has an 85.0% pct yield, we need to multiply the moles by a gene of

\[{\rm{n}}\;{\rm{(salicylic acid)}}\;{\rm{ = }}\;{\rm{111}}\;{\rm{mol}}\;{\rm{ \times }}\;\frac{{{\rm{100}}}}{{{\rm{85}}}}\;{\rm{ = }}\;{\rm{131}}\;{\rm{mol}}\]

The mass of salicylic acid would be:

\[{\rm{1000}}\;{\rm{(salicylic acid)}}\;{\rm{ = }}\;{\rm{131}}\;{\rm{mol}}\;{\rm{ \times }}\;\frac{{{\rm{138}}\;{\rm{g}}}}{{{\rm{ane}}\;{\rm{mol}}}}\;{\rm{ = }}\;{\rm{18,078}}\;{\rm{yard}}\]

This corresponds to 1.81 kg

Stoichiometry Worksheet 1 Mass Mass,

Source: https://general.chemistrysteps.com/stoichiometry-practice-problems/

Posted by: plumbupasylat.blogspot.com

Share this post